2.5. Analog ouput (DAC)
1. Introduction
A PWM output can be easily transformed into an “analog” signal using low-pass filtering. This is the reason why Arduino calls its PWM output as analog. Nevertheless, the STM32F072 device features a real Digital to Analog Converter (DAC). When using DAC, you get closer to a real analog output as we will see in this tutorial.
2. DAC setup
According to the device datasheet, there are two pins that can be used as DAC output: PA4 and PA5. As PA5 is already used by the board LED, we will only consider DAC Channel 1, attached to PA4.

For a basic functionality, the DAC setup is very simple. You just need to setup PA4 pin as analog, then turn on DAC clock and enable DAC. That’s all. Add the following function to your bsp.c and the associated declaration to bsp.h:
/*
* DAC_Init()
* Initialize DAC for a single output
* on channel 1 -> pin PA4
*/
void BSP_DAC_Init()
{
// Enable GPIOA clock
RCC->AHBENR |= RCC_AHBENR_GPIOAEN;
// Configure pin PA4 as analog
GPIOA->MODER &= ~GPIO_MODER_MODER4_Msk;
GPIOA->MODER |= (0x03 <<GPIO_MODER_MODER4_Pos);
// Enable DAC clock
RCC->APB1ENR |= RCC_APB1ENR_DACEN;
// Reset DAC configuration
DAC->CR = 0x00000000;
// Enable DAC Channel 1
DAC->CR |= DAC_CR_EN1;
}
3. Sampling period setup
We want to output an analog sample from the DAC at regular time interval. Because we are unsure of the time it takes to compute sample, we will use a timer update event to trigger new samples on a regular basis. Adjust the previously developed TIM6 time base function so that update event (detected by polling UIF flag) occurs every 200µs:
/*
* BSP_TIMER_Timebase_Init()
* TIM6 at 48MHz
* Prescaler = 48 -> Counting period = 1µs
* Auto-reload = 200 -> Update period = 200µs
*/
void BSP_TIMER_Timebase_Init()
{
// Enable TIM6 clock
RCC->APB1ENR |= RCC_APB1ENR_TIM6EN;
// Reset TIM6 configuration
TIM6->CR1 = 0x0000;
TIM6->CR2 = 0x0000;
// Set TIM6 prescaler
// Fck = 48MHz -> /48 = 1MHz counting frequency
TIM6->PSC = (uint16_t) 48 -1;
// Set TIM6 auto-reload register for 200µs period
TIM6->ARR = (uint16_t) 200 -1;
// Enable auto-reload preload
TIM6->CR1 |= TIM_CR1_ARPE;
// Start TIM6 counter
TIM6->CR1 |= TIM_CR1_CEN;
}
4. Sinewave output
In the example bellow, the DAC is used to output a sinewave.
...
#include <math.h>
...
// Main program
int main()
{
float angle, y;
uint16_t output;
// Configure System Clock
SystemClock_Config();
// Initialize LED pin
BSP_LED_Init();
// Initialize DAC output
BSP_DAC_Init();
// Initialize 200µs time base
BSP_TIMER_Timebase_Init();
// Initialize variables
angle = 0.0f;
while(1)
{
// Start measure
BSP_LED_On();
// Increment angle value modulo 2*PI
angle = angle + 0.01f;
if (angle > 6.28f) angle = 0.0f;
// Compute sinus(angle)
y = sinf(angle);
// Offset and Scale output to DAC unsigned 12-bit
output = (uint16_t)(0x07FF + (int16_t)(0x07FF * y));
// End measure
BSP_LED_Off();
// Set DAC output
DAC->DHR12R1 = output;
// Wait for update event (one sample every 200µs)
while ((TIM6->SR & TIM_SR_UIF) == 0);
TIM6->SR &= ~TIM_SR_UIF;
}
}
The samples are calculated on-the-fly using the sinf() function from <math.h> library. sinf() is faster than sin() because it is written using simple precision floats instead of double precision floats.
The angle variable goes from 0 to 6.28 ($2\pi$, for those who wonder) by steps of 0.01 providing us with 628 samples for one period. Given that we have a 200µs period between samples, the sinewave period is:
$f=\frac{1}{628\times 200µs}=7.9617 Hz$
The sinf() function returns a float number y in the range [-1 : 1]. The DAC data register is an unsigned 12-bit number [0 : 4095] that represents voltage between 0 and 3.3V. Therefore, for a full-scale 3.3Vpp sinewave, we have:
$DAC_{output}=2047+(y\times 2047)$
Last thing, note that LED on PA5 is used to measure the time it takes to the CPU to compute and output the next sinus sample. We can use this to make sure that processing time is below the 200µs sampling period. If not, we have a problem...
Everything should be clear now. Save all ![]() , build
, build ![]() , and run
, and run ![]() the application.
the application.
Probe PA4 and PA5 with an oscilloscope, and you should see this. The sinewave frequency and amplitude are in perfect agreement with the anticipated values.
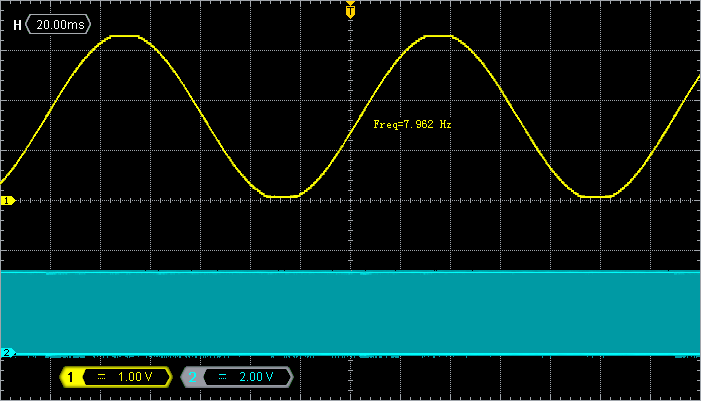
The application uses the LED pin to provide a measure of time required to compute a new sample. This method to measure execution time is simple and precise. You must use it whenever you need. Probing PA5 (channel 2 of the oscilloscope) reveals that the math part of the code requires between 56µs to 104µs to complete depending on the value of angle. The time the sinf() function takes to deliver result is therefore not deterministic and depends on its operand. This is something usual you need to know.
The application will execute as expected as long as the sampling period accommodates the longest sample processing time. Here, 200µs are well enough to cope with sample calculation. Otherwise, the uniformity of the sampling is lost.
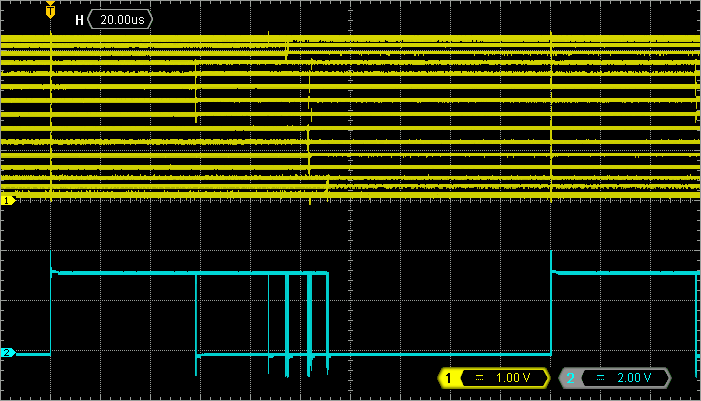
If you want to try the standard sin() function, you need to change the time base to allow about 300µs between update events. The sin() function takes between 100µs to 200µs to complete.
This is quite a long time, and the reason why math functions should be used with care when timing constraints are tight. Otherwise, you can use a Look-Up table (more on that later), or if you are rich, buy you a better CPU with hardware floating point unit (FPU). Cortex-M4 CPUs have one…
 | - - |
5. Summary
This short tutorial introduced the DAC peripheral and uniform sampling of digitized signals. It is a groundwork for further signal processing applications.

Add new comment